Transformer的时间和空间复杂度都是和输入句子长度的平方,这种平方的时间、空间复杂度使得Transformer难以建模很长的序列。因此Transformer发布之后,很多研究者研究如何降低Attention中的复杂度,在不影响效果的前提下,使得Attention在时间和空间复杂度上达到线性的。Luna也是线性化Attention的尝试。Luna主要在Transformer基础上做了两点改变,将标准Attention实现线性化:(1)增加一个额外的固定长度为$l$的输入序列lP;(2)使用两个Attention,分别是Pack Attention和Unpack Attention,一个用来将长度为$n$的输入序列X压缩成固定长度的序列,另一个则是用来将这个固定长度的序列解压缩成原来长度的序列。通过这两点时间复杂度从原来的$O(N^2)$降低到了$O(ln)$。由于l是一个超参数,因此时间复杂度是线性的。
回顾Transformer
传统的Attention机制可以用如下的公式表示:
$$
Y = Attn(X, C) = \omega( \frac{XW_Q(CW_K)^T} {\sqrt{d}} )CW_V
$$
注意力函数Attn输入两个序列$X \in R^{n \times d}$ 和 $C \in R^{m \times d} $,输出序列$Y \in R^{n \times d}$。其中的$n,m$表示序列长度,$d$表示特征维度。$W_q, W_k, W_v \in R^{d \times d}$是三个可学习的网络参数,用于将两个输入序列映射成Query,Key,Value:$Q=XW_Q,K=CW_K,V=CW_V$。$\omega$是激活函数,通常是$softmax$。公式计算出来的矩阵$A = \omega( \frac{XW_Q(CW_K)^T} {\sqrt{d}} ) \in R^{m \times n}$即常说的注意力矩阵,用来表示输入序列$X$和$C$中任意两个token之间的对齐分数。
Attention是Transformer模型的重要组成部分,除此之外还有position wise feed-forward network(FFN)和layer normalization。有了这三个组件,Transformer的层的定义即可用如下公式表示:
$$
X_A = LayerNorm(Atten(X, C) + X)
$$
$$
X^{\prime} = LayerNorm(FFA(X_A) + X_A)
$$
Linear Unified Nested Attention (Luna)
Luna的层与标准Transformer的层区别如下图。整体来看,Luna相比于Transformer多了一条“边路”,用于对额外的输入序列$P \in R^{l \times d}$进行学习。其次,Luna Attention由两个Attention组成,并且这两个Attention存在交叉,这两个Attention就是Pack Attention和Unpack Attention。
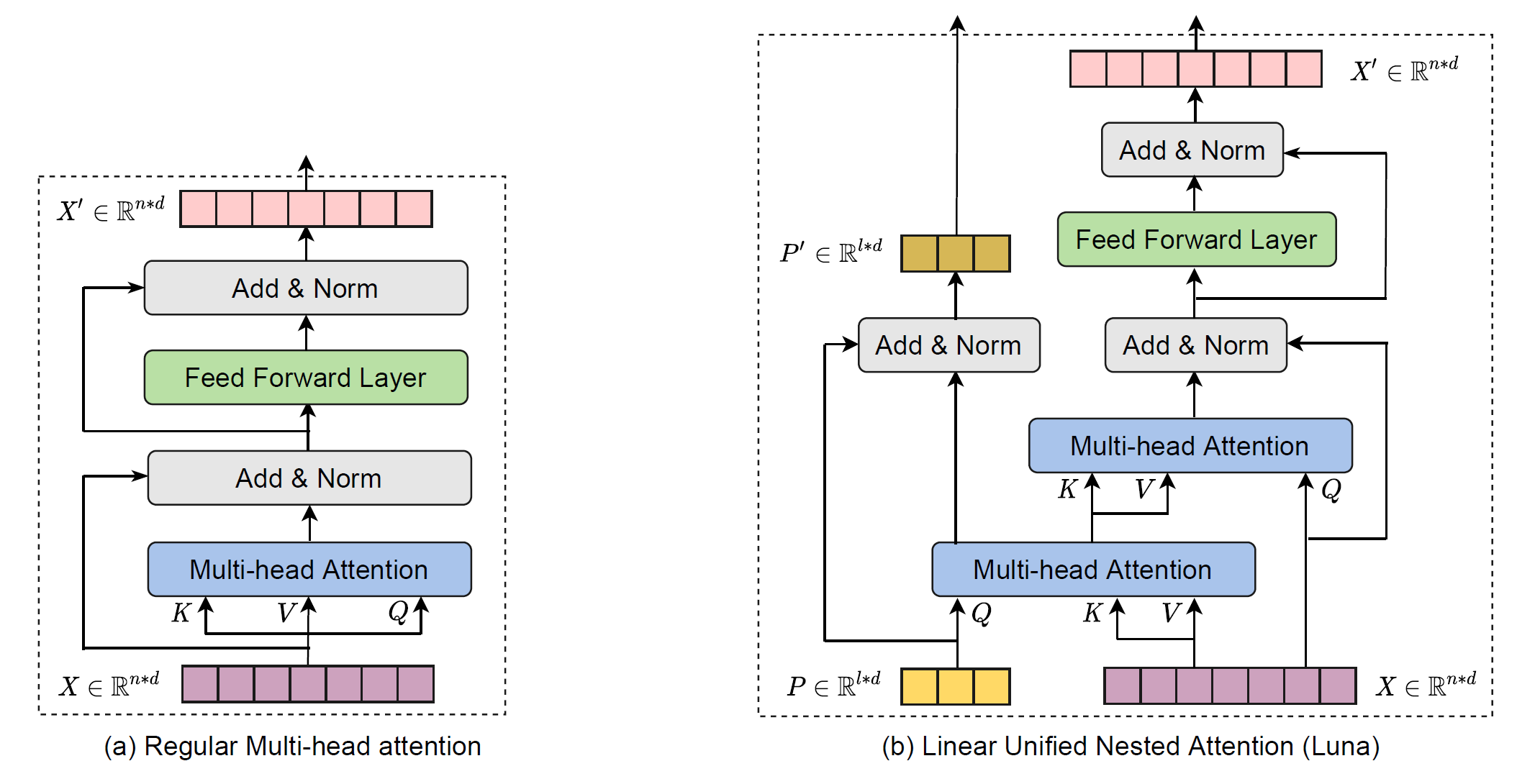
Pack Attention将输入序列$X \in R^{n \times d}$压缩成长度为$l$的序列$Y_P \in R^{l \times d}$:
$$
Y_P = Attn(P,C)
$$
Unpack Attention则将$Y_P$解压缩成原始长度的序列:
$$
Y_X = Attn(X, Y_P)
$$
最终,Luna中使用的Attentiion可以表示为:
$$
Y_X,Y_P = LunaAttn(X,P,C)
$$
类似Transformer层的定义,将LunaAttn和FFN,LayerNorm结合起来,可以得到Luna层的定义:
$$
Y_X,Y_P = LunaAttn(X,P,C)
$$
$$
X_A,P_A = LayerNorm(Y_X + X),LayerNorm(Y_P + P)
$$
$$
X^{\prime}, P^{\prime} = LayerNorm(FFN(X_A) + X_A), P_A
$$
到这里,Luna层的定义已经介绍完了。
Luna Causal Attention
这里不知道如何翻译Causal Attention这个名词。不过Causal Attention要做的事情很简单:为了能够支持自回归解码,注意力机制在计算时应该只利用当前token以及当前token以前的token的信息,而不应该利用当前token之后的信息,因为在解码当前token时,未来的token是什么还是未知的。
由于Luna Attention使用Pack Attention将输入序列压缩成了另一个长度更短的序列,因此不能像标准的self-attention一样直接mask掉之后的token。
为了设计这样一个causal attention,作者首先假设了$P$不包含$X$的信息,并且定义了causal函数$f: R^{n \times d_1} \times R^{n \times d_1} \times R^{n \times d_2} \rightarrow R^{n \times d_2}$:
$$
F \triangleq f(X,Y,Z), where F_t = \frac{1}{t}X_t\sum_{t=1}^tY_j^TZ_j
$$
$F \in R^{n \times d_2}$,并且$F_t$表示矩阵$F$的第t行。从$F$的定义可以看到,矩阵$F$的第t行表示了输入$X,Y,Z$第t行以及第t行以前的token的信息。
有了上面的定义,可以通过如下的步骤实现causal attention。首先计算pack attention:$A_{pack}=\omega(\frac{PX^T}{\sqrt{d}})$(省略了$W_Q,W_K,W_V$)。在计算$A_{pack}$时,激活函数$\omega$不能使用softmax,因为这样在计算某个token时会使用这个token后续token的信息。因此作者借鉴了Linear Transformer的做法,将激活函数定义为$\omega(\cdot)=elu(\cdot)+1$。接着使用causal函数计算unpack attention:$A_{unpack}=f(X,X,A_{pack}^T)$,这里的激活函数可以使用softmax,因为这里的softmax是针对l进行的,而不是针对n进行的。最终的输出Y可以表示为:$Y=f(A_{unpack}, A_{pack}^T, X)$。
实验结果
这里简单看看实验结果。主要关注长文本序列建模能力,时间消耗和模型在自然语言理解任务上的效果。
长文本序列建模
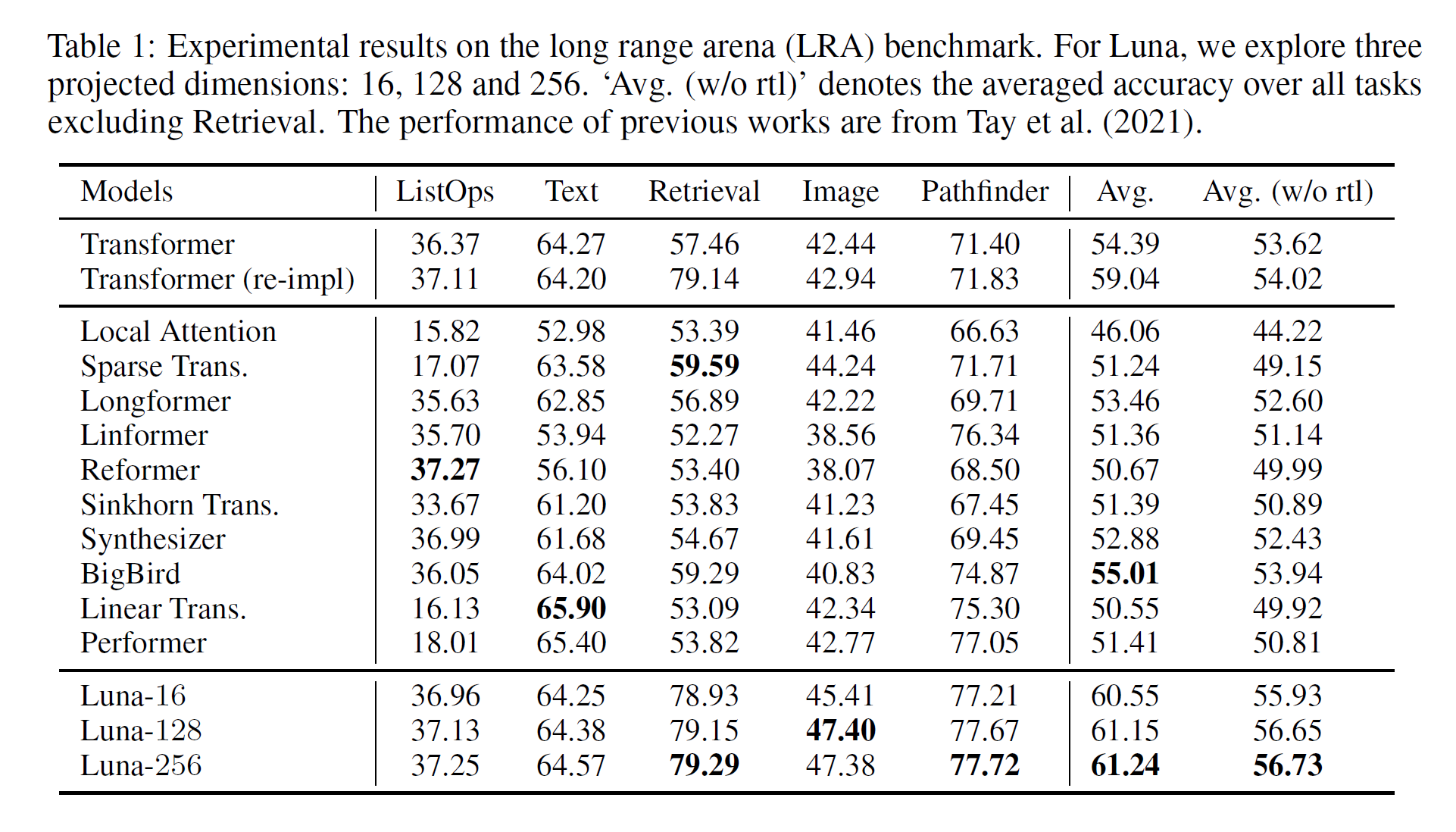
长文本序列建模在标准数据集LRA上进行。从实验效果上看,所有任务都取得了比Transformer好的效果,平均准确率也超过了所有比较的模型。
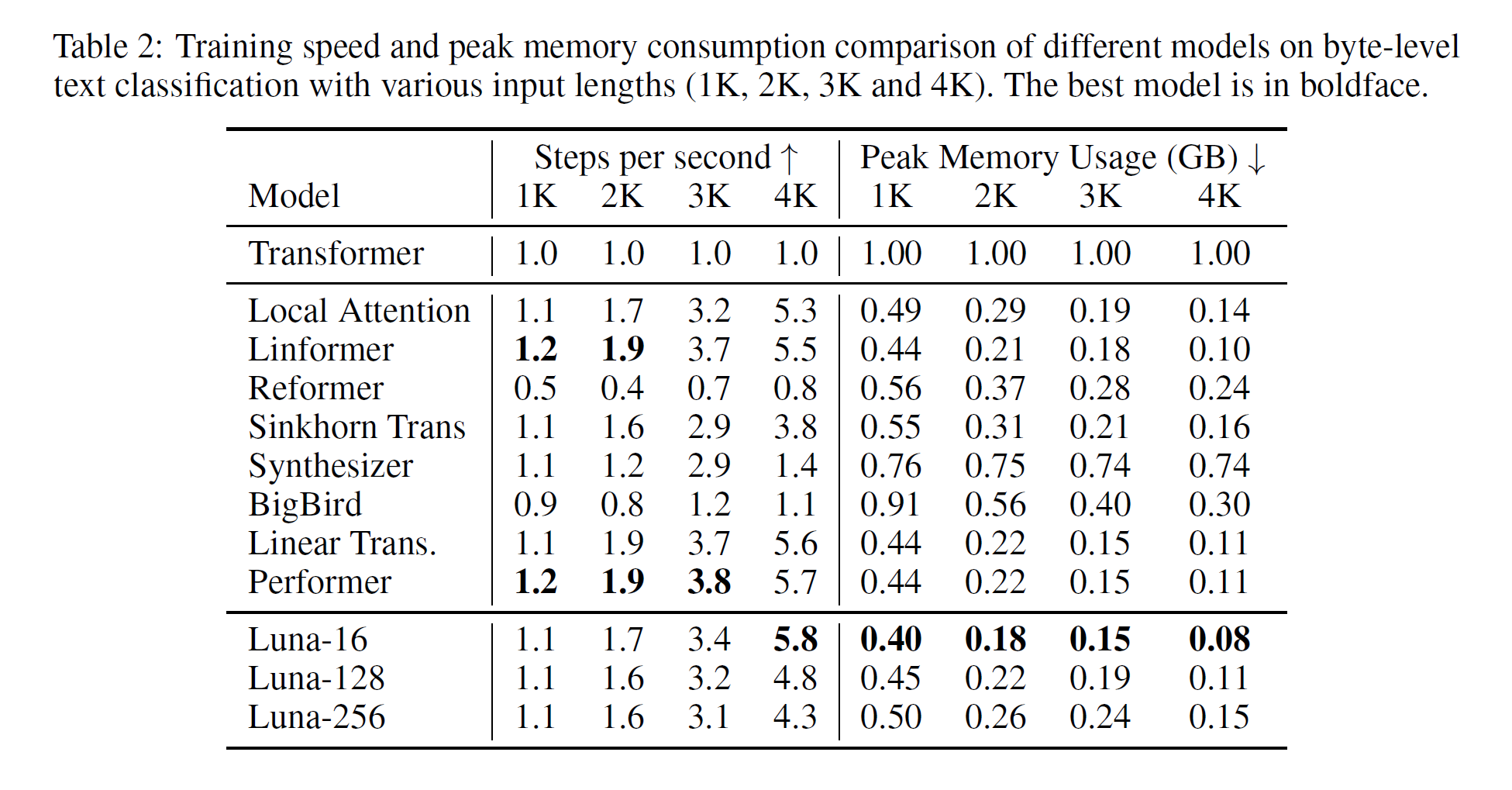
内存方面,各种不同长度输入序列消耗的内存相比于Transformer的比例如下图所示。Luna-16相比于其他比较模型取得了最好的效果,占用内存最小。但是Luna-256没有太大优势。这里的实验比较个人认为有些问题,在进行内存占用比较时,作者用Luna-16来进行比较,但是由于Luna-16参数量小,效果上并不是最好的。因此,Luna并没有做到内降低内存的同时,还保证效果。当Luna模型的参数量上来的时候,内存占用并没有太大的优势。
预训练
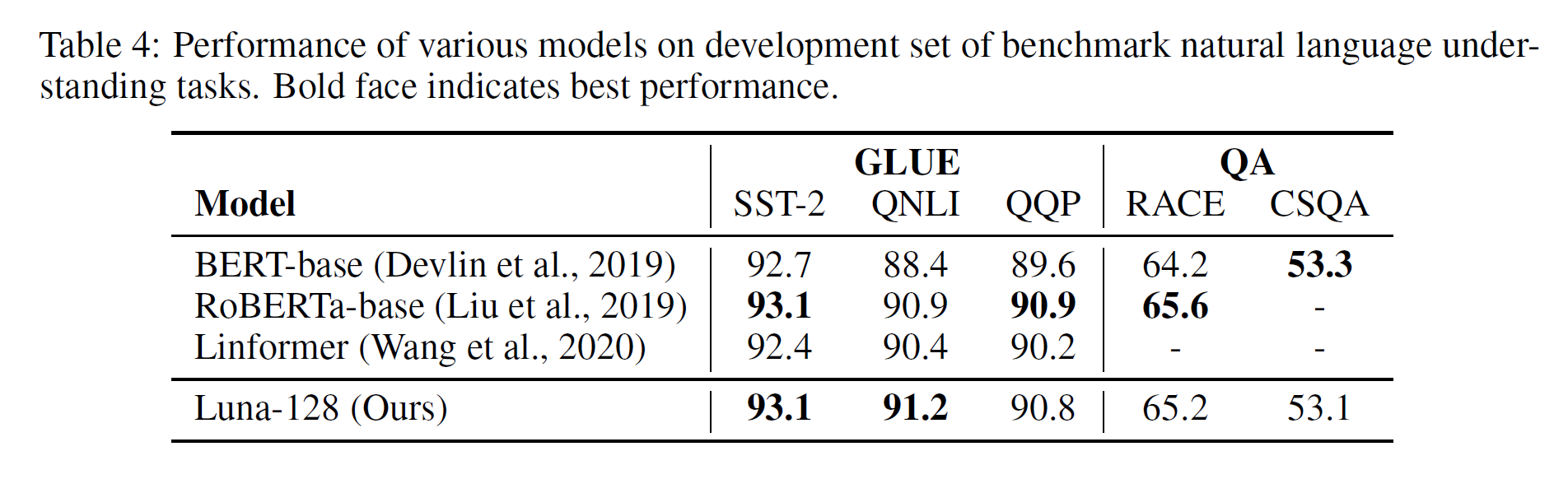
预训练任务是先在大规模预料上进行预训练,然后在各种下游任务上进行微调。这部分实验在GLUE和QA任务上进行。
从实验结果可以看到,Luna和其他模型相比,效果上并没有太大差别。当然了,出来Linformer外,其他使用的都是标准softmax,而Luna则是使用了线性化的Attention。Luna能够做到在节省时间和空间的前提下效果不降就已经是“好”的效果了。
总结
Luna是线性化Attention的尝试,通过嵌套的两个attention来达到线性化的目的。这里线性化的实现是因为多了一个额外输入$P$,其序列长度$l$是预先定义的,因此时间和空间复杂度可以降到$O(ln)$。但是,当输入序列长度$n$很长是,$l$设定为一个合理的值,模型才能得到较好的效果,因此本质上$l$还是一个和$n$相关的参数。所以,这里是否真的做到了线性化的时间和空间,还有待商榷。
