Transformer-XL是Transformer模型的变种，主要用于解决长序列的建模问题。Transformer-XL可以看作是Transformer+RNN的结合体，不同的是Transformer-XL的递归是基于一个文本片段进行的。此外，Transformer-XL还引入了相对位置编码，以解决在Transformer中老生常谈的关于位置信息的问题。

问题

Transformer模型抛弃了常用的RNN，CNN的方式完全采用自注意力的方式来对数据进行建模，这种方式

$O(n^2)$的时间空间复杂度

Transformer中使用的dot-product自注意力计算公式如下：

$$
Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V
$$

其中，$Q,K,V \in R^{n \times d}$，所以$softmax(\frac{QK^T}{\sqrt{d_k}}) \in R^{n \times n}$，n是输入序列的长度。这意味着时间和空间复杂度都是$O(n^2)$，那么随着输入序列长度的增加，时间和空间的消耗都会平方级的增加。由于这个原因，Transformer难以建模很长的序列。

上下文碎片化问题

当然了，虽然时间和空间复杂度很高，但是在输入序列不是很长的情况下，我们依旧可以将一个很长的序列分成几段，然后一段一段的输入模型，从而实现对长序列的建模，facebook曾经就是这么搞的Al-Rfou et al(2018)。这个过程可以用论文中下面这张图来说明：

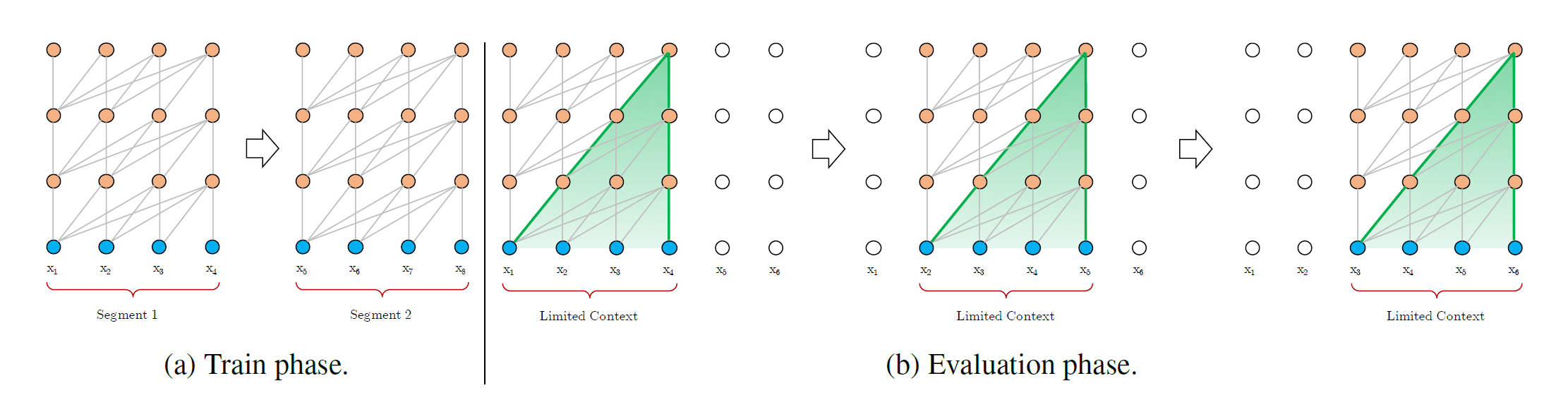
对于输入序列$X=[x_1, x_2, …, x_8]$一共8个词，每4个词为一段，则一共有两个segment需要输入模型。假设Transformer每次只能输入4个词，那么在训练阶段，依次将两个片段输入即可。在推理阶段，则以4个词大小的滑动窗口，从输入序列$X$中从左到右滑过，每次移动一个词的距离，并且依次将滑动窗口内的词作为输入，即可获得这个序列的输出。

那么可以看到，在训练过程中片段和片段之间是没有交互的，这就是作者观察到的上下文碎片化问题。其次，在inference阶段，由于每次仅移动一个词，那么当序列很长的时候，inference的速度也会很慢。

基于上面提到的问题，作者Transformer基础上引入片段级递归和相对位置编码，提出了Transformer-XL，使得模型可以建模较长的序列。

模型介绍

片段级递归

作者在Transformer架构上引入了循环机制，不过相比于RNN仅保留上一个词的hidden state作为

假设两个连续的长度都是L的输入片段为：$s_t=[x_{t,1},x_{t,2},…,x_{t, L}]$和$s_{t + 1}=[x_{t + 1,1},x_{t + 1,2},…,x_{t + 1,L}]$，同时将第n层layer对第$t$个输入序列$s_t$计算得到的hidden state表示为$h_t^n \in R^{L \times d}$，其中$d$表示特征的维度。那么第n层的第$t + 1$个输入片段$s_{t + 1}$的hidden state可以通过下面的公式计算得到：

$$
\widetilde h_{t + 1}^{n - 1} = [ SG( h_t^{n-1} ) \circ h_{t+1}^{n-1}]
$$

$$
q_{t+1}^n = h_{t+1}^{n-1}W_q^T
$$

$$
k_{t+1}^n=\widetilde h_{t+1}^{n-1}W_k^T
$$

$$
v_{t+1}^n=\widetilde h_{t+1}^{n-1}W_v^T
$$

$$
h_{t + 1}^{n} = TransformerLayer(q_{t + 1}^n, k_{t + 1}^n, v_{t + 1}^n)
$$

函数$SG(\dot)$表示stop-gradient，$[h_v \circ h_v]$表示将两个hidden state沿着序列长度的维度进行拼接，$W$表示模型的参数。需要注意的是，$q_{t + 1}^n \in R^{L \times d}$，而$k_{t + 1}^n, v_{t + 1}^n \in R^{2L \times d}$，所以最终得到的$h_{t + 1}^n \in R^{L \times d}$。

上面提到的就是Transformer-XL引入的片段级递归机制。另外需要注意这里引入的片段级递归机制与传统的RNN语言模型的递归有所不同。传统的RNN语言模型的递归是在同一层实现的，即当前的hidden state包含了前面所有tokens的语言信息。但是在Transformer-XL中，$h_{t + 1}^n$和$h_t^{n-1}$之间的依赖是跨层的，所以随着层数的增加，最终模型才能够“看”到更多的上下文。

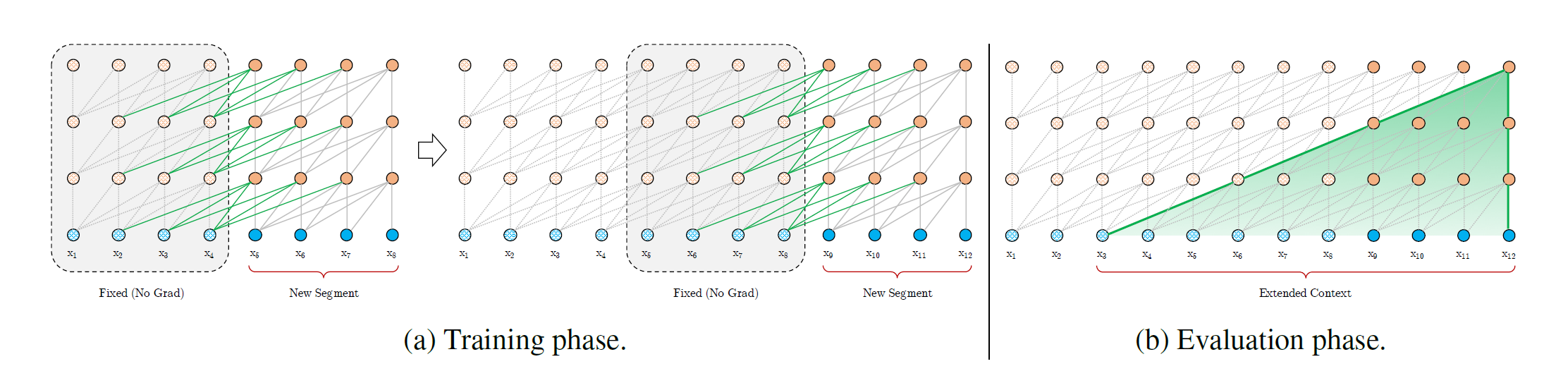
相对位置编码

为了能够重用hidden state，还有一个问题尚未解决。即位置编码的问题。Transformer使用绝对位置编码来表示每个token的位置，但是由于Transformer-XL将一个长序列分成多个片段，每个片段依次送入Transformer中，那么这样模型没有足够的信息区分不同片段的相同位置。

为了解决这个问题，作者引入了相对位置编码。

首先来看看在标准的Transformer中，$q_i$和$k_j$的注意力分数是如何依赖于绝对位置编码的。我们用$U \in R^{L_{max} \times d}$表示绝对位置编码的矩阵，其中$L_{max}$表示最大序列长度，$d$表示位置编码向量的维度，那么第i行就表示的是第i个位置的绝对位置向量。$q_i$和$k_j$的注意力分数就可以通过如下公式计算：

$$A_{i,j}^{abs} = E_{x_i}^T W_q^T W_k E_{x_j} + E_{x_i}^TW_q^TW_kU_j + U_i^TW_q^TW_kE_{x_j} + U_i^TW_q^TW_kU_j$$

上式中等号右边四项依次记为(a),(b),(c),(d)。作者对上面基于绝对位置编码计算attention的公式做了对应的修改，以在attention计算中加入相对位置编码：

$$
A_{i,j}^{rel} = E_{x_i}^T W_q^T W_{k,E} E_{x_j} + E_{x_i}^TW_q^T W_{k,R} R_{i-j} + u^T W_{k,E} E_{x_j} + v^T W_{k,R} R_{i-j}
$$

加入相对位置编码的attention主要有以下几项改变：

• 将(b)、(d)两项中的关于绝对位置编码的部分$U_i,U_j$替换为$R_{i-j}$，即原来的绝对位置向量现在用两个词之间的相对位置向量来表示。
• 在(c)项中引入了可训练的参数$u \in R^d$，代替原来的$U_i^T W_q^T$。这意味着相同的词在不同的位置将表示相同的含义。(d)项中也引入了参数$v \in R^d$替换$U_i^T W_q^T$。
• 将原来的参数$W_k$分成了$W_{k,R},W_{k_E}$。其中$W_{k,E}$用来生成基于内容的key向量，而$W_{k,R}$用来生成基于位置的key向量。